解析Bitcoin與Layer2資產跨鏈技術
原文標題:AdaptorSignaturesandItsApplicationtoCross-ChainAtomicSwaps
原文鏈接:https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/
作者:mutourend,lynndell1.引言
隨著BitcoinLayer2擴容方案的快速發展,Bitcoin與其Layer2對應網絡之間的跨鏈資產轉移頻率顯著增加。這一趨勢受到Layer2技術(如Bitlayer)所提供的更高可擴展性、更低的交易費和高吞吐量的推動。這些進步促進了更高效、更經濟的交易,從而促進Bitcoin在各種應用中的更廣泛采用和集成。因此,Bitcoin與Layer2網絡之間的互操作性正成為Crypto生態系統的關鍵組成部分,推動創新,并為用戶提供更多多樣化和強大的金融工具。
如表1所示,Bitcoin與Layer2之間的跨鏈交易有三個典型方案,分別為中心化跨鏈交易、BitVM跨鏈橋和跨鏈原子交換。這三個技術在信任假設、安全性、便捷性、交易額度等方面各不相同,能滿足不同的應用需求。
表1.跨鏈交易技術對比


Schnorr/ECDSA適配器簽名的預簽名均對隨機數$r$進行承諾=rG。此外,零知識證明中對隨機數$v$進行承諾$=vG,V=vY$。如果隨機數泄漏,則會導致私鑰泄漏。
具體而言,在Schnorr協議中,如果隨機數$r$泄漏,則能夠根據等式
$ =r+cx.$
計算出私鑰$x$。
同理,在ECDSA協議中,如果隨機數$r$泄漏,則能夠根據等式
$=r^{-1}(hash(m)+R_xx).$
計算私鑰出$x$。
最后,在零知識證明協議中,如果隨機數$v$泄漏,則能夠根據等式
$z:=v+cr.$
計算出隨機數$r$,從而進一步根據隨機數$r$計算出私鑰$x$。因此,隨機數使用完后需立刻刪除。3.1.2隨機數重用問題
對任意兩個跨鏈交易,如果適配器簽名協議使用相同的隨機數,則會導致私鑰泄漏。具體而言,在Schnorr協議中,如果使用了相同的隨機數$r$,則以下方程組中僅$r$和$x$是未知的
$_1=r+c_1x,$
$_2=r+c_2x.$
因此,可以求解方程組,獲得私鑰$x$。
同理,在ECDSA適配器簽名協議中,如果使用相同的隨機數$r$,則以下方程組中僅$r$和$x$是未知的
$_1=r^{-1}(hash(m_1)+R_xx),$
$_2=r^{-1}(hash(m_2)+R_xx).$
因此,可以求解方程組,獲得私鑰$x$。
最后,在零知識證明協議中,如果使用相同的隨機數$v$,則以下方程組中僅$v$和$r$是未知的
$z_1=v+c_1r,$
$z_2=v+c_2r.$
因此,可以求解方程組,獲得隨機數$r$,從而進一步解方程組獲得私鑰$x$。
以此類推,不同用戶使用相同的隨機數,也會泄漏私鑰。換言之,使用相同隨機數的兩個用戶,能夠求解方程組,獲得對方的私鑰。因此,應使用RFC6979解決隨機數重用問題。3.1.3解決方案:RFC6979
RFC6979指定了一種使用DSA和ECDSA生成確定性數字簽名的方法,解決了與生成隨機值k相關的安全問題。傳統的DSA和ECDSA簽名依賴于每次簽名操作隨機生成的隨機數k。如果此隨機數被重用或生成不當,會危及私鑰的安全性。RFC6979通過從私鑰和待簽名消息中確定性地導出$k$,消除了生成隨機數的需求。這確保了使用相同私鑰簽署相同消息時,簽名總是相同的,從而增強了可重現性和可預測性。具體而言,確定性的$k$是由HMAC生成的。該過程涉及哈希函數(例如SHA256)對私鑰、消息和計數器計算哈希值,
$k=SHA256(sk,msg,counter).$
上述等式中,為表達簡潔,僅對私鑰sk,消息msg和計數器counter計算哈希值,實際RFC6979中計算過程涉及更多的哈希計算。該等式確保k對每條消息都是唯一的,同時對于相同的輸入具有可重現性,并且減少了與弱或受損的隨機數生成器相關的私鑰暴露風險。因此,RFC6979為使用DSA和ECDSA的確定性數字簽名提供了一個強大的框架,解決了與隨機數生成相關的重大安全問題,并增強了數字簽名的可靠性和可預測性。這使其成為需要高安全性和符合嚴格操作要求的應用程序的寶貴標準。Schnorr/ECDSA簽名存在隨機數缺陷,需要使用RFC6979進行防范。因此,基于Schnorr/ECDSA的適配器簽名也存在這些問題,也需要使用RFC6979規范以解決這些問題。3.2跨鏈場景問題與解決方案3.2.1UTXO與賬戶模型系統異構問題與解決方案
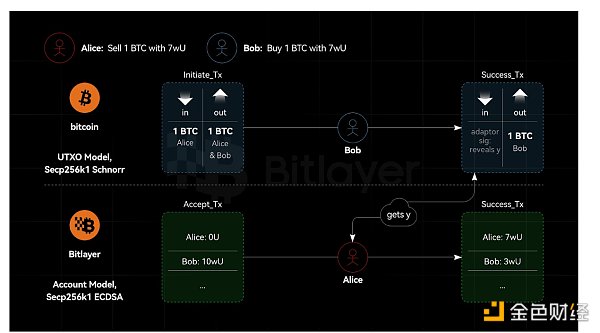
如圖1所示,Bitcoin采用UTXO模型,基于Secp256k1曲線實現原生的ECDSA簽名。Bitlayer為EVM兼容BitcoinL2鏈,采用Secp256k1曲線,支持原生的ECDSA簽名。適配器簽名實現了BTC交換所需的邏輯,而Bitlayer交換對應方則由Ethereum智能合約的強大功能支撐。
基于適配器簽名的跨鏈原子交換,或至少是設計用于ECDSA曲線的semi-scriptless適配器簽名方案,與Ethereum不兼容。原因在于Ethereum是賬戶模型的,而不是UTXO模型。具體而言,基于適配器簽名的原子交換中要求退款交易必須預先簽名。但是,在Ethereum系統中,如果不知道nonce,則無法預先簽名交易。因此,一方可以在預先簽名完成和交易執行之間發送交易——這將使預先簽名的交易無效(因為nonce已被使用,不能重復使用)。
此外,從隱私角度來看,這意味著Bitlayerswap的匿名性比HTLC更優(swap的雙方都可找到合約)。但是,由于需要一方有公開合約,使得Bitlayerswap的匿名性低于適配器簽名的匿名性。在沒有合約的一方,swap交易看起來與任何其他交易都一樣。但是,在有EVM合約的一方,交易明顯是為了資產swap。雖然一方有公開合約,但是即使使用復雜的鏈分析工具,也不可能將其追溯到另一條鏈。
3.2.3不同曲線,適配器簽名不安全
假設Bitcoin使用Secp256k1曲線和ECDSA簽名,而Bitlayer使用ed25519曲線和Schnorr簽名。該情況下,不能使用適配器簽名。由于曲線不同,導致橢圓曲線群的階不同,即模系數不同。Bob在Bitcoin系統中將$y$適配到ECDSA簽名中時,即計算$s:=+y$。此時,$y$的取值空間為Secp256k1橢圓曲線群的標量空間。隨后,Alice需要使用$y$在ed25519橢圓曲線群上進行Schnorr簽名。但是,ed25519曲線余因子為8,且模系數不等于Secp256k1橢圓曲線群的模系數。因此,使用$y$在ed25519曲線上進行Schnorr簽名是不安全的。4.數字資產托管應用
數字資產托管有三個參與方,分別為:買方Alice、賣方Bob和托管方。使用適配器簽名能夠實現非交互式門限數字資產托管,且在無需交互的情況下實例化門限支出策略的子集。該子集由2種參與者組成:參與初始化的參與者、不參與初始化的參與者,后者稱為托管方。托管方不能簽署任意交易,而只向支持的其中一方發送秘密。
一方面,托管人只能在幾個固定的結算交易中進行選擇,而無法與其他參與方之一簽署新的交易。因此,這種秘密釋放機制使得非交互式門限托管的靈活性不如門限Schnorr簽名。另一方面,可以使用門限Schnorr簽名設置2-of-3花費策略。但是,門限Schnorr簽名協議需要三方運行進行Decentralization密鑰生成協議。因此,基于適配器簽名的資產托管協議具有非交互優勢。4.1基于適配器簽名的非交互式資產托管
圖3.基于適配器簽名的非交互式資產托管
如圖3所示,Alice和Bob想要創建一個具有隱形策略的2-of-3交易輸出,其中包含一個托管方。取決于條件$c$,Alice或Bob可花費該交易輸出。如果Alice和Bob之間存在爭議,則托管方(公鑰為$E$,私鑰為$e$)決定由Alice或Bob獲得該資產。
創建一個未簽名funding交易,將BTC發送給Alice和Bob之間的某2-of-2MuSigoutput。
Alice選擇一個隨機值$t_A$,將某交易的adapator為$t_A G$的Schnorr預簽名$(\hat{R}_A,\hat{s}_A)$發送給Bob,該交易為將fundingoutput發送給Bob。Alice同時給Bob發送一個密文,該密文包含對秘密$t_A$并將托管公鑰$E$調整為$E_c=E+hash(E,c)G$的\textbf{可驗證加密}$C=Enc(E_c,t_A)$。該過程中,Bob收到Alice的預簽名后,加上自己的簽名,不滿足2-of-2MuSig,從而無法花費fundingoutput。僅當Bob知道$t_A$(由托管方可提供),或Alice另外簽署完整簽名發送給Bob,才能花費fundingoutput。
與之相對應,Bob基于其adaptorsecret$t_B$,重復步驟(2)。此時Bob所簽的交易為將fundingoutput發送給Alice。
Alice和Bob均驗證接收密文的有效性,確認密文是對$E_c$對秘密的加密,從而對funding交易簽署并廣播。可驗證加密使得在setup階段無需托管方參與,且不需要公開合約$c$。
當有爭議時,Alice和Bob可將密文以及條件c發送給托管方,則托管方可實際情況判決,從而使用調整私鑰$e+hash(E,c)$進行解密發送$t_A/t_B$給Bob/Alice。
如果無爭議,則Alice和Bob可按其所想來花費2-of-2MuSigoutput。如果存在爭議,則任何一方均可聯系托管方,并請求其adaptorsecret$t_A$或$t_B$。因此,其中一方在托管方的幫助下,可完成該適配器簽名,并廣播該結算交易。4.2可驗證加密
基于離散對數的經典可驗證加密方案(PracticalVerifiableEncryptionandDecryptionofDiscreteLogarithms)不能用于Secp256k1adaptors,因其僅支持驗證特殊結構化的groups。
目前,有2種有前景的方式來基于Secp256k1離散對數做可驗證加密,分別為Purify和Juggling。
Purify最初是為了創建具有確定性nonce(DN)的MuSig協議而提出的,要求每個簽名者使用零知識證明其nonce是將偽隨機函數(PRF)正確應用于公鑰和消息的結果。PurifyPRF可在Bulletproofs零知識協議的算術電路中高效實現,用于在Secp256k1上的離散對數創建可驗證加密方案。換言之,使用zkSnark實現可驗證加密。
Juggling加密包括四個步驟:(1)將離散對數$x$切分為多個長為$l$的片段$x_k$,使得$x=\sum_k2^{(k-1)l}x_k$;(2)使用公鑰$Y$對片段$x_k G$進行ElGamal加密$\{D_k,E_k\}=\{x_k G+r_k Y,r_k G\}$;(3)對每個$x_k G$創建范圍證明,證明$D_k$為一個Pedersen承諾$x_k G+r_k Y$,且其值小于$2^l$;(4)使用sigma協議,證明$\{sumD_k,sumE_k\}$是對$x_k G$的正確加密。
在解密過程中,對$\{D_k,E_k\}$解密出每個$x_k G$,然后窮舉搜索出$x_k$(取值范圍為$[0,2^l)$)。
Purify需在Bulletproofs內執行一個PRF,相對復雜,而Juggling理論上更簡單。此外,二者在proofsize、證明時長和驗證時長的差距很小。5.總結
本文對Schnorr/ECDSA適配器簽名與跨鏈原子交換的原理進行了詳細描述。深入分析了適配器簽名存在隨機數泄漏問題、重復問題,并提出使用RFC6979以解決這些問題。此外,詳細分析了跨鏈應用場景下,不但應考慮Blockchain的UTXO模型與賬戶模型之間的區別,還應考慮適配器簽名是否支持不同算法、不同曲線等問題。最后,對適配器簽名進行擴展應用,實現非交互式數字資產托管,并簡單介紹了涉及的密碼學原語--可驗證加密。
參考文獻
GuggerJ.Bitcoin-monerocross-chainatomicswap[J].CryptologyePrintArchive,2020.
FournierL.One-timeverifiablyencryptedsignaturesakaadaptorsignatures[J].2019,2019.
https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf
PorninT.Deterministicusageofthedigitalsignaturealgorithm(DSA)andellipticcurvedigitalsignaturealgorithm(ECDSA)[R].2013.
KomloC,GoldbergI.FROST:flexibleround-optimizedSchnorrthresholdsignatures[C]//SelectedAreasinCryptography:27thInternationalConference,Halifax,NS,Canada(VirtualEvent),October21-23,2020,RevisedSelectedPapers27.SpringerInternationalPublishing,2021:34-65.
https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md
https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps/
CamenischJ,ShoupV.Practicalverifiableencryptionanddecryptionofdiscretelogarithms[C]//AnnualInternationalCryptologyConference.Berlin,Heidelberg:SpringerBerlinHeidelberg,2003:126-144.
NickJ,RuffingT,SeurinY,etal.MuSig-DN:Schnorrmulti-signatureswithverifiablydeterministicnonces[C]//Proceedingsofthe2020ACMSIGSACConferenceonComputerandCommunicationsSecurity.2020:1717-1731.
ShlomovitsO,LeibaO.Jugglingswap:scriptlessatomiccross-chainswaps[J].arXivpreprintarXiv:2007.14423,2020.
